Exercise: Vehicle suspension system modeling and input response

From FBSwiki
Jump to: navigation, search

(Contributed by Demetri Spanos and Haomiao Huang, 3 Oct 04)

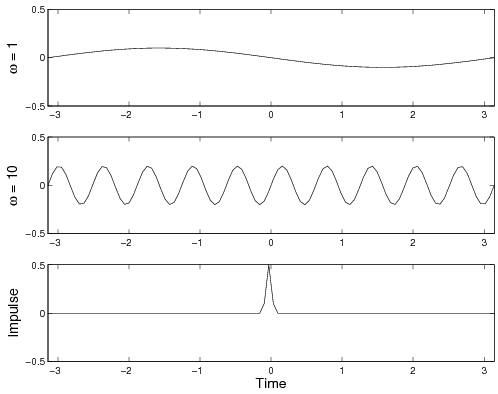
In this problem we will explore a simple example of a suspension system for a vehicle. In general, mechanical systems respond differently to different inputs. One categorization of inputs is in terms of "frequency content". We will analytically study a simple mechanical system to understand its response to the three kinds of inputs shown in the figure below:

Three inputs.png

One aspect of a car's dynamics is the interaction of the car chassis with the suspension. As a crude model, we will treat the chassis as a lumped mass 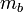, and the suspension as a linear stiffness with constant . We will also assume that the suspension includes a viscous damper (shock-absorber) with damping coefficient 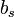. Newtonian mechanics gives the following differential equation for the body dynamics:

math

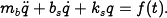
Here, 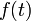is the input force from the ground. The three inputs shown represent relatively smooth road, very bumpy road, and a single isolated bump.

  1. Setting 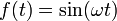, analytically solve the differential equation for the steady-state solution, in terms of the system parameters 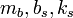, and the driving frequency 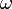. Assume 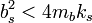so that the system is underdamped (typical of this kind of mechanical system).

  2. Sketch the amplitude of the steady-state response as function of the driving frequency . Identify the maximum of this plot in terms of the model parameters.

  3. The parameters that enter a model influence its behavior. Consider the limiting cases 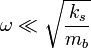and 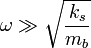. What does your amplitude plot tell you about the response to these two different frequencies? What about inputs near this frequency?

  4. The third input shown is called an "impulse", and is usually modeled as discontinuously altering the velocity of the system. This happens, for example, when driving over a sharp step in elevation. Setting 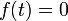, solve the differential equation with initial conditions 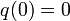, , 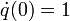as a function of the system parameters. Again assume the system is underdamped.

  5. Do you see any relationship between the oscillation frequency of this solution and the amplitude plot for the steady-state solution?

  6. What do your answers above tell you about the role of the car's mass in reducing the effect of impulsive disturbances?

Retrieved from "https://www.cds.caltech.edu/~murray/amwiki/Exercise:_Vehicle_suspension_system_modeling_and_input_response&oldid=2937"