Poster Abstracts
B
Stochastic Variational Integrators
Nawaf Bou-Rabee (Applied Mathematics, California Institute of Technology)
Abstract:
In this poster we introduce a simple stochastic mechanical system which exhibits ballistic diffusion, and apply various variational partitioned Runge-Kutta methods to numerically compute its statistical properties. In particular, we numerically compute the rate of convergence of the empirical distribution to the equilibrium Gibbs measure, and the mean squared displacement of the mechanical system. This numerical experiment is designed to evaluate the performance of stochastic variational integrators at computing the correct long-time statistical properties of a stochastic mechanical system.
C
A Microscopic Model of Viscous Friction
Guido Cavallaro (Mathematics, University of Rome "La Sapienza")
Cavallaro Poster
Abstract:
Consider a body moving along the  -axis under the action of an external force
-axis under the action of an external force 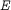 and immersed in an infinitely extended perfect gas. Assume the gas to be described by the mean-field approximation and interacting elastically with the body. In this set up, we discuss the following statement: ``Let
and immersed in an infinitely extended perfect gas. Assume the gas to be described by the mean-field approximation and interacting elastically with the body. In this set up, we discuss the following statement: ``Let 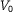 be the initial velocity of the body and
be the initial velocity of the body and 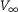 its asymptotic velocity, then for
its asymptotic velocity, then for 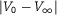 small enough it results
small enough it results 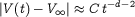 for
for  large, where
large, where 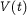 is the velocity of the body at time
is the velocity of the body at time  ,
,  the dimension of the space and
the dimension of the space and 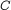 is a positive constant depending on the medium and on the shape of the body''.
is a positive constant depending on the medium and on the shape of the body''.
The reason for the power law approach to the stationary state instead of the exponential one (usually assumed in viscous friction problems), is due to the long memory of the dynamical system.
In a recent paper by Caprino, Marchioro and Pulvirenti, it has been discussed the case of 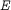 constant and positive, with
constant and positive, with 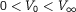 , for a disk orthogonal to the
, for a disk orthogonal to the  -axis. We have completed the analysis in the cases
-axis. We have completed the analysis in the cases 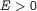 with
with 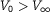 and
and  . We have also approached the problem of an
. We have also approached the problem of an  -dependent external force, by choosing
-dependent external force, by choosing 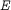 of harmonic type. In this case we obtain the power-like asymptotic time behavior for the body position
of harmonic type. In this case we obtain the power-like asymptotic time behavior for the body position 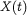 . The investigation, done in detail for a disk orthogonal to the
. The investigation, done in detail for a disk orthogonal to the  -axis, can be extended to a body with a general convex shape.
-axis, can be extended to a body with a general convex shape.
G
Affine Euler-Poincar� and Lie-Poisson reductions. Application to perfect complex fluids.
Fran�ois Gay-Balmaz (Mathematics, EPFL)
Abstract:
As opposed to the case of perfect (simple) fluids, the dynamics of
perfect complex fluids depends also on variables called order parameters that
describe the macroscopic variations of the internal structure of the fluid
parcels. These macroscopic variations may form observable patterns, as seen in
liquid crystals. Other examples of perfect complex fluids include superfluids,
Yang-Mills magnetofluids and spin-glasses.
From a serie of papers by Holm, Marsden and Ratiu, it is known that the Euler-
Poincar� framework provides a unified approach for fluids and leads to new
models.
We extend this framework to the case of perfect complex fluids by:
(1) adding an affine term to the cotangent lifted action,
(2) replacing the group of fluid motions by a semidirect product of this group
and the Lie group of order parameters.
We also explore the Hamiltonian counterpart of the problem and obtain, using
the process of reduction by stages, that the symplectic reduced spaces are
affine coadjoint orbits.
Three regularizations as turbulent subgrid models
Jonathan Pietarila Graham (NCAR and the Univ. of Colorado)
Collaborators: Darryl Holm, Pablo Mininni, and Annick Pouquet
Abstract:
Geophysical and astrophysical phenomena involve a huge range of
scales. The number of degrees of freedom are inconceivable for
numerical simulations to achieve, and truncation of the omitted scales
removes important physics. Regularization subgrid models for this
closure problem have recently emerged. Unlike many Large Eddy
Simulations (LES), these models have guarantees on the computability
of their solutions, conserve energy, and recover the physical
equations as the filter width vanishes.
Three regularizations can be viewed as LES with successively more
complex subgrid-stress terms: the Clark, Leray, and alpha models.
Comparing these, we establish the affects of each term. As each has
different small-scale energy spectra this can shed light on the link
between small-scale properties of the flows and their intermittent
behavior. We find that Leray fails to recover large-scale anisotropy
in our flow and the time scale for the development of turbulence.
The Clark and alpha models both perform well in these regards but require
extra dissipative for adequate computational gains. We also test the
helicity of vortex tubes, Beltramization of the flow, and statistical
properties for the subgrid models.
K
'''Direct simulation and regularization modelling of rotating turbulence
Arkadiusz K Kuczaj''' (Mathematics, University of Twente)
Collaborators: Bernard J. Geurts and Darryl D. Holm
Kuczaj Poster
Abstract:
Rotation considerably affects the dynamics and the structure of turbulence through the Coriolis force. This leads to two-dimensionalization of the flow at high rotation rates. The presented numerical investigation analyzes the application of regularization models for fundamental studies of turbulence in a rotating frame of reference, and at high Reynolds numbers. Numerical experiments are conducted using Leray and LANS-alpha models and compared with DNS results. Particular attention is given to the flow structuring, the energy decay law and the reduced energy transfer to small scales for various rotation rates.
L
On a new inviscid regularization of the 3D Navier-Stokes and Euler equations
Boris Levant (Weizmann Institute)
Abstract:
In this work I consider the Navier-Stokes-Voght (NSV) model of viscoelastic fluid, which was recently proposed as a new type of regularization for the 3D Navier-Stokes equations. I will discuss the question of the well posedness of the model and show that the global attractor of the NSV equations, driven by the analytic forcing, consists of analytic functions. Moreover, in order to provide additional evidences that the NSV model can indeed be used to study the statistical properties of the 3D Navier-Stokes equations, I will present the results of the numerical study of the Sabra shell model of turbulence, to show that for the small value of the regularizations parameter one recovers the anomalous inertial range scaling.
A study of the Navier-Stokes-alpha model for two-dimensional turbulence
Evelyn Lunasin (University of California, Irvine)
Collaborators: Susan Kurien, Mark Taylor, and Edriss S. Titi
Lunasin Poster
Abstract:
The Navier-Stokes-alpha sub-grid scale model of turbulence is a mollification of the Navier-Stokes equations in which the vorticity is advected and stretched by a smoothed velocity field. The smoothing is performed by filtering the velocity field over spatial scales of size smaller than alpha. This is achieved by convolution with a kernel associated with the Green's function of the Helmholtz operator scaled by a parameter alpha. The statistical properties of the smoothed velocity field are expected to match those of Navier-Stokes turbulence for scales larger than alpha, thus providing a more computable model for those scales.
For wavenumbers 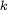 such that
such that 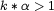 , corresponding to spatial scales smaller than alpha, there are three candidate power laws for the energy spectrum, corresponding to three possible characteristic time scales in the model equations: one from the smoothed field, the second from the rough field and the third from a special combination of the two. Using two-dimensional turbulence as a test case, we measure the scaling of the spectra from high-resolution simulations of the Navier-Stokes-alpha model, in the limit as alpha goes to infinity. We show that the energy spectrum of the smoothed velocity field scales as
, corresponding to spatial scales smaller than alpha, there are three candidate power laws for the energy spectrum, corresponding to three possible characteristic time scales in the model equations: one from the smoothed field, the second from the rough field and the third from a special combination of the two. Using two-dimensional turbulence as a test case, we measure the scaling of the spectra from high-resolution simulations of the Navier-Stokes-alpha model, in the limit as alpha goes to infinity. We show that the energy spectrum of the smoothed velocity field scales as 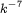 in the direct enstrophy cascade regime, consistent with dynamics dominated by the time scale of the rough velocity field. We conclude by giving some possible explanations to this result. In addition, we also present the corresponding results for the two-dimensional Leray-alpha model.
in the direct enstrophy cascade regime, consistent with dynamics dominated by the time scale of the rough velocity field. We conclude by giving some possible explanations to this result. In addition, we also present the corresponding results for the two-dimensional Leray-alpha model.
M
The Inverse Problem for Invariant Lagrangians on a Lie Group
Tom Mestdag (Mathematics, University of Michigan)
Abstract:
The inverse problem of Lagrangian mechanics consist of finding a regular Lagrangian for a given set of second-order differential equations on a manifold. In this paper, we focuss on the case that the manifold is in fact a Lie group and discuss a restricted type of inverse problem: for an invariant second-order system, when does there exist a Lagrangian which is invariant under left (or right) translations? Our framework relies on a reduction of the second-order system on the Lie group to a first-order system on the corresponding Lie algebra. We conclude with some illustrative examples.
P
Optimal Rearrangements for Ocean Data Assimilation
James Percival (Mathematics, Imperial College, London)
Abstract:
Data Assimilation is process of combining real observations of a dynamical system with numerical models of the same or similar systems, in order to generate analyses of the current system state and to predict future behaviour. When assimilating data it is important to preserve as many known constraints and conservation properties as possible, however many traditional methods for ocean data assimilation often destroy known material conservation properties. Results from rearrangement theory allow calculation of an optimal analysis state through polar factorization, but this allows for physically unrealistic rearrangement and fails when observations do not cover the whole domain. Instead we present two iterative methods for generating an analysis rearrangement, analogous to 3 dimensional and 4 dimensional variational assimilation. Results are shown from identical twin studies with a two layer quasi-geostrophic ocean model, showing the quantitative an qualitative superiority of the rearrangement method in most cases.
T
A geometric approach for nonlocal dissipation in the Vlasov equation
Cesare Tronci (Mathematics, Imperial College, London)
Abstract:
We introduce nonlocal dissipation into the Vlasov equation by using the methods of [1] and [2]. The result we find differs from a similar equation of [3] and [4] in that it admits single-particle solutions for the Vlasov distribution. Applications are suggested for galactic dynamics and charged particle dynamics, where single-particle solutions are vital. Upon extending our framework to Vlasov moments, we find a nonlocal dissipative version of the Benney long-wave system in hydrodynamics.
[1] Holm, Darryl D.; Putkaradze, Vakhtang, Formation and evolution of singularities in anisotropic geometric continua, arXiv.org/nlin.AO/0608054.
[2] Holm, Darryl D.; Putkaradze, Vakhtang; Tronci, Cesare, Geometric order parameter equations, in preparation.
[3] Kandrup, Henry E., The secular instability of axisymmetric collisionless star clusters, Astrophys. J., 380, (1991), no. 2, part 1.
[4] Bloch, Anthony; Krishnaprasad, P. S.; Marsden, Jerrold E.; Ratiu, Tudor S., The Euler-Poincar� equations and double bracket dissipation, Comm. Math. Phys., 175, (1996), no. 1.



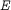
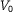
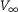
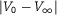
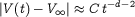


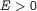
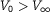

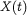
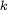 such that
such that 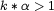 , corresponding to spatial scales smaller than alpha, there are three candidate power laws for the energy spectrum, corresponding to three possible characteristic time scales in the model equations: one from the smoothed field, the second from the rough field and the third from a special combination of the two. Using two-dimensional turbulence as a test case, we measure the scaling of the spectra from high-resolution simulations of the Navier-Stokes-alpha model, in the limit as alpha goes to infinity. We show that the energy spectrum of the smoothed velocity field scales as
, corresponding to spatial scales smaller than alpha, there are three candidate power laws for the energy spectrum, corresponding to three possible characteristic time scales in the model equations: one from the smoothed field, the second from the rough field and the third from a special combination of the two. Using two-dimensional turbulence as a test case, we measure the scaling of the spectra from high-resolution simulations of the Navier-Stokes-alpha model, in the limit as alpha goes to infinity. We show that the energy spectrum of the smoothed velocity field scales as 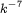 in the direct enstrophy cascade regime, consistent with dynamics dominated by the time scale of the rough velocity field. We conclude by giving some possible explanations to this result. In addition, we also present the corresponding results for the two-dimensional Leray-alpha model.
in the direct enstrophy cascade regime, consistent with dynamics dominated by the time scale of the rough velocity field. We conclude by giving some possible explanations to this result. In addition, we also present the corresponding results for the two-dimensional Leray-alpha model.