|
|
Textbooks, References, and Topics
Course Text
- R. Abraham, J. E. Marsden, and T. Ratiu, Manifolds, Tensors, Analysis, and Applications, Second Edition. Springer-Verlag, 1988. (Draft Third Edition, Current Update started January 3, 2007)
Note: Links go to version cds202-08
Lecture Notes and Supplements
Additional references that may be useful:
- Anthony Bloch, Nonholonomic Mechanics and Control, Springer Verlag.
- W. Boothby, An Introduction to Differentiable Manifolds and Riemannian Geometry, 2nd ed. Academic Press, 1986.
- V. Guillemin and A. Pollak, Differential Topology, Prentice-Hall, 1974.
- J.M. Lee, Introduction to Smooth Manifolds, Springer-Verlag, 2002.
- J. Milnor, Topology From the Differentiable Viewpoint, University Press of Virginia, 1965.
- B. Schutz, Geometrical Methods of Mathematical Physics, Cambridge University Press, 1980.
- M. Spivak, A Comprehensive Introduction to Differentiable Geometry, vol I. Publish or Perish, 1970.
- F.W. Warner, Foundations of Differentiable Manifolds and Lie Groups, Springer-Verlag, 1983.
Course Topics
- Motivation for geometric methods: general, historic introduction; example of pendulum: introduce manifolds as configuration spaces; differentiation leads to notion of tangent space; vector fields on manifolds as fundamental object; and, Lie groups as symmetry groups.
- Topology: motivation; metric spaces; topological spaces; mappings between topological spaces; properties.
- Differential manifolds: topological manifolds; charts;
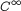 -manifolds; examples; constructing manifolds; open submanifold; product manifolds. -manifolds; examples; constructing manifolds; open submanifold; product manifolds.
- Mappings between manifolds: diffeomorphisms, submersions, immersions.
- Submanifolds: open, immersed, imbedded, and regular submanifolds; mention Whitney Imbedding Theorem.
- Tangent space: link geometric intuition with formal definition; pull-back; push-forward; coordinate transformations.
- Tangent bundle: fiber bundles, sections; distributions.
- Vector fields: integral curves; flow of a vector field; coordinate-free definition of dynamical system.
- Lie algebras: Lie derivative; Jacobi-Lie bracket; Lie algebras; role in control of nonlinear systems.
- Frobenius theorem
- Lie groups
- Covector fields: dual of vector space; covectors and covector fields; pull-back of covector field.
- Lie derivatives
- Tensors
- Riemannian manifolds
- Exterior algebra
- Manifolds with boundaries
- Integration on manifolds
- Discrete exterior calculus
|
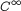 -manifolds; examples; constructing manifolds; open submanifold; product manifolds.
-manifolds; examples; constructing manifolds; open submanifold; product manifolds.
