Abstracts
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V |
W | X | Y | Z |
D
Scientific computing using streaming processors
Eric
Darve
Abstract:
In recent years, several companies such as NVIDIA, ATI,
ClearSpeed, and IBM-Toshiba-Sony have released a new generation of
processors based on a streaming architecture. These processors achieve
an unprecedented level of performance by using a large number of light
cores able to concurrently process data. The most spectacular success
in that direction are graphics cards from NVIDIA and ATI. Even though
they were originally developed for graphics applications, they are
capable of many general purpose computing tasks. We have been
investigating the use of these processors for scientific computing. We
will outline the capabilities of these processors and the constraints
they impose on the type of algorithms which can run efficiently. These
processors require significantly rethinking the way algorithms and
data structures are designed. In our last project, we have developed
code to solve the compressible Euler equations on a GPU. We will
describe some of the techniques developed for this simulation. We
performed a simulation of a 3D hypersonic vehicle at Mach 5 with 1.5
million mesh nodes. The measured speed-up was 20x compared to a
conventional one core processor.
F
Stability of Asynchronous Variational Integrators
Will
Fong
Abstract:
The formulation of multiple-time-step integrators can provide substantial computational savings for mechanical systems with multiple time scales. However, the scope of these savings may be severely limited by the range of allowable time step choices. We have performed an exhaustive study of the linear stability of the fully asynchronous methods called AVI (asynchronous variational integrator), with two time steps, for essentially any combination of their values. In addition we have obtained approximate analytical expressions for the time step ratios that may render the scheme unstable in the case of linear equations, and verified them with extensive numerical computations. Synchronous multiple time stepping schemes such as r-RESPA show resonances when the outer step is a multiple of the effective half period of one of the fast oscillators. An elegant generalization is derived in the fully asynchronous case of AVI.
K
Discrete Variational Fluids
Eva
Kanso
Abstract:
The variational principles for incompressible fluid mechanics are best
expressed in a Lagrangian formalism. However, computational efficiency
calls for an Eulerian treatment of fluids to avoid the numerical
issues inherent to deforming meshes. An Eulerian variational treatment
of discrete fluids is extremely delicate due to restriction on
variations in the Eulerian formalism. In this talk, we will present
our recent attempts towards developing discrete variational fluids and
discuss our successes and failures. In particular, we propose a
computationally-tractable discretization of the fundamental
configuration space, i.e., the group of volume preserving
diffeomorphisms, in terms of the group of doubly stochastic matrices.
Alas, a fully-Eulerian variational formulation based on this novel
discretization fails to produce an accurate fluid integrator. We then
propose the use of a material representation of the fluid motion (a
discrete inverse map) and discuss how this idea may be used to develop
discrete variational fluids.
DMOC and Robotic Systems
Marin
Kobilarov
Abstract:
The talk is about the optimal control of systems with symmetries and nonholonomic constraints in a discrete mechanics setting. Along with a standard direct approach, an alternative solution method is introduced based on higher-order conditions. Computational efficiency is addressed in terms of the choice of formulation (direct vs indirect), coordinate (free) representation, choice of initial trajectory, and trajectory refinement scheme. Applications to rigid body groups and to simple robotic models (an RC helicopter and a car-like robot) are presented.
L
A discontinuous-Galerkin-based immersed boundary method
Adrian
Lew
Abstract:
A numerical method to approximate partial differential equations on meshes that do not conform to the
domain boundaries is introduced. The proposed method is conceptually simple and free of user-defined
parameters, and has optimal order of convergence. This is shown through numerical experiments in
reaction-diffusion and elasticity problems.
Variational integrators and optimal control of constrained systems
Sigrid
Leyendecker
Abstract:
From the variety of methods to enforce holonomic constraints in the
framework of Lagrangian dynamics, the focus is on the Lagrange multiplier method
and a null space method, both yielding exact constraint fulfilment. These
methods can be used in conjunction with a variational integrator leading
to a discrete trajectory which, besides respecting a discrete symplectic
structure and conserving discrete momentum maps exactly, also shows good energy behaviour.
However the two methods differ significantly in the dimension of the
system of nonlinear equations, condition number of the
iteration matrix during the iterative solution procedure and computational
costs, whereby the discrete system resulting from the discrete null
space method perform excellently in the mentioned categories. In particular, it
has the minimal possible dimension making it exceptionally well-suited
to be used as equality constraints in a nonlinear
optimisation problem which determines the actuation forces. Together
with initial and final conditions on the configuration and conjugate momentum, they serve as nonlinear equality
constraints for the minimisation of a given cost functional. The algorithm
yields a sequence of discrete configurations together with a sequence of
actuating forces, optimally guiding the system from the initial to the desired
final state.
M
Foliation Processing
Alex McKenzie,
Patrick Mullen
Abstract:
We present a purely Eulerian framework for variational geometry processing of surfaces and foliations. Instead of focusing on a single isosurface as in the Level Set method (LSM), we process all isosurfaces at once (i.e., the foliation induces by the level set) to achieve a variational treatment of basic interface motions like mean curvature flow (MCF). At the core of our approach is the use of the Coarea Formula (a classical result of Geometric Measure Theory) to express area integrals over isosurfaces as volume integrals. With this formula, our treatment of MCF no longer has to rely on LSM-like finite differences, but is achieved via a true minimization of "Eulerian surface area" of the foliation-based interface. A simple Petrov-Galerkin approach to more general gradient flows will be presented. Numerical tests demonstrate an improved accuracy compared to LSM, and we hope to exploit these initial results to offer a better handling of free surface flows with surface tension, without the traditional use of smoothed Dirac functions at the interface (and the delicate trade-offs involved in their use).
N
Constructing point vortex equilibria via Brownian ratchets
Paul
Newton
Abstract:
We pose the problem of how to find the positions and strengths of 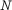 particles in the plane that interact via
a logarithmic Hamiltonian so that the configuration moves as a rigid body (i,e. relative equilibria).
If written as a dynamical system for the
particles in the plane that interact via
a logarithmic Hamiltonian so that the configuration moves as a rigid body (i,e. relative equilibria).
If written as a dynamical system for the  interparticle distances, the problem can be
formulated as one in linear algebra. Solve
interparticle distances, the problem can be
formulated as one in linear algebra. Solve 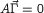 , where
, where  is an
is an 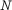 by
by 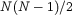 non-normal (
non-normal (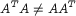 ) `configuration matrix', and
) `configuration matrix', and 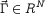 is the vector of
particle strengths. We do this by performing a singular value decomposition on
is the vector of
particle strengths. We do this by performing a singular value decomposition on  (i.e. calculate
the eigenvalues of the covariance matrix
(i.e. calculate
the eigenvalues of the covariance matrix 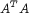 ) for an arbitrary initial configuration, then use
the smallest non-zero singular value as a ratchet, driving it to zero (guaranteeing that
) for an arbitrary initial configuration, then use
the smallest non-zero singular value as a ratchet, driving it to zero (guaranteeing that  will have a
non-empty nullspace) by allowing the particles to undergo a random walk in
will have a
non-empty nullspace) by allowing the particles to undergo a random walk in 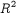 and keeping only those
new configurations that decrease the smallest singular value until it drops below some convergence
threshold. The final distribution of non-zero singular values allows us to calculate the Shannon
entropy of the configuration (a measure of its disorder), its size as measured by Frobenius norm,
and the `distance' between two different equilibrium configurations. Joint work with George Chamoun.
and keeping only those
new configurations that decrease the smallest singular value until it drops below some convergence
threshold. The final distribution of non-zero singular values allows us to calculate the Shannon
entropy of the configuration (a measure of its disorder), its size as measured by Frobenius norm,
and the `distance' between two different equilibrium configurations. Joint work with George Chamoun.
P
Discrete Mechanics and Optimal Control for the Compass Biped
David
Pekarek
Abstract:
A methodology for generating locally optimal control policies for simple hybrid mechanical systems is presented and demonstrated on the compass gait biped. Principles from discrete mechanics are utilized so that optimal control policies may be generated as the solution to constrained nonlinear optimization problems. In the context of bipedal walking, this procedure provides a comparative measure of the suboptimality of existing control policies. Furthermore, the methodology can potentially be used as a tool for designing controlled trajectories that are locally optimal with respect to both continuous and discrete behaviors.
S
DEC and AVIs for Computational Electromagnetism
Ari
Stern
Abstract:
In classical field theory, Maxwell's equations have an elegant,
coordinate-free Lagrangian formulation in terms of spacetime
differential forms. However, many methods of computational
electromagnetism fail to preserve this geometric structure, resulting
in spurious modes and other numerical difficulties. Using discrete
exterior calculus (DEC) to discretize the classical spacetime forms,
we derive a general family of variational integrators for Maxwell's
equations. These methods include the well-known Yee scheme as a
special case, but also generalize to irregular spacetime meshes,
including a new asynchronous variational integrator (AVI) for
electromagnetism. These methods preserve both the variational
structure and the differential forms structure of the continuous
theory, and consequently, they are multisymplectic, have discrete
gauge symmetry, and conserve the associated momentum map
(i.e. conservation of charge).
W
Cutoff phenomena in Markov Chain models of chaotic mixing
Matt
West
Abstract:
We explore the connections between mixing in fluid flows, chaotic maps and Markov Chains. For Markov Chain mixing, the cutoff phenomenon has been much studied in recent years, whereby the system experiences a sharp transition from unmixed to mixed as time evolves. We consider chaotic maps and fluid flows in the limit of zero diffusion and provide analytical and numerical evidence to support the conjecture that cutoff also occurs in such systems.

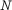 particles in the plane that interact via
a logarithmic Hamiltonian so that the configuration moves as a rigid body (i,e. relative equilibria).
If written as a dynamical system for the
particles in the plane that interact via
a logarithmic Hamiltonian so that the configuration moves as a rigid body (i,e. relative equilibria).
If written as a dynamical system for the  interparticle distances, the problem can be
formulated as one in linear algebra. Solve
interparticle distances, the problem can be
formulated as one in linear algebra. Solve 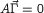 , where
, where  is an
is an 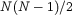 non-normal (
non-normal (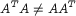 ) `configuration matrix', and
) `configuration matrix', and 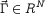 is the vector of
particle strengths. We do this by performing a singular value decomposition on
is the vector of
particle strengths. We do this by performing a singular value decomposition on 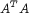 ) for an arbitrary initial configuration, then use
the smallest non-zero singular value as a ratchet, driving it to zero (guaranteeing that
) for an arbitrary initial configuration, then use
the smallest non-zero singular value as a ratchet, driving it to zero (guaranteeing that 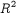 and keeping only those
new configurations that decrease the smallest singular value until it drops below some convergence
threshold. The final distribution of non-zero singular values allows us to calculate the Shannon
entropy of the configuration (a measure of its disorder), its size as measured by Frobenius norm,
and the `distance' between two different equilibrium configurations. Joint work with George Chamoun.
and keeping only those
new configurations that decrease the smallest singular value until it drops below some convergence
threshold. The final distribution of non-zero singular values allows us to calculate the Shannon
entropy of the configuration (a measure of its disorder), its size as measured by Frobenius norm,
and the `distance' between two different equilibrium configurations. Joint work with George Chamoun.