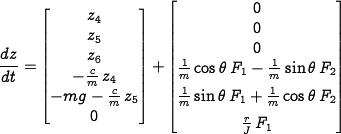Vectored thrust aircraft
This page documents the (planar) vertical takeoff and landing (PVTOL) aircraft model that is used as a running example throughout the text. A detailed description of the dynamics of this system is presented in Chapter 2 - System Modeling, with control analysis and design performed in Chapter 6 - State Feedback and Chapter 11 - Frequency Domain Design. This page brings together this material into a single place, to illustrate the application of analysis and design tools for this system. Links to MATLAB scripts are included that generate the analysis and figures described here.
System Description
Consider the motion of vectored thrust aircraft, such as the Harrier "jump jet" shown below (left). The Harrier AV-8B military aircraft redirects its engine thrust downward so that it can "hover" above the ground. Some air from the engine is diverted to the wing tips to be used for maneuvering.

|

|
A simplified model of the Harrier is shown above (right), where we focus on the motion of the
vehicle in a vertical plane through the wings of the aircraft.
We
resolve the forces generated by the main downward thruster and the
maneuvering thrusters as a pair of forces 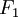 and
and 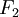 acting at a
distance
acting at a
distance  below the aircraft (determined by the geometry of the
thrusters).
below the aircraft (determined by the geometry of the
thrusters).
Let 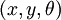 denote the position and orientation of the center
of mass of the aircraft.
Let
denote the position and orientation of the center
of mass of the aircraft.
Let 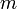 be the mass of the vehicle,
be the mass of the vehicle, 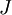 the moment of inertia,
the moment of inertia, 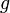 the
gravitational constant and
the
gravitational constant and  the damping coefficient. Then the
equations of motion for the vehicle are given by
the damping coefficient. Then the
equations of motion for the vehicle are given by
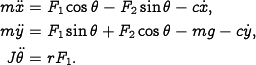
It is convenient to redefine the inputs so that the origin is an
equilibrium point of the system with zero input. Letting 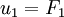 and
and 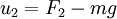 , the equations become
, the equations become
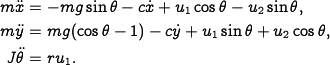
These equations describe the motion of the vehicle as a set of three coupled second-order differential equations.
LQR state feedback controller
This section demonstrates the design of an LQR state feedback controller for the vectored thrust aircraft example. This example is pulled from Chapter 6 - State Feedback.
- pvtol_lqr.m - MATLAB code used to produce figures in this example
- pvtol_params.m - parameter definitions
See the software page for more information on how to run these scripts.
The dynamics of the system can be written in state space form as
|
The system parameters are shown at the right and correspond to a scaled model of the system.
The equilibrium point for the system is given by 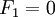 ,
, 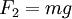 and
and 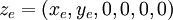 . To derive the linearized
model near an equilibrium point, we compute the linearization at
. To derive the linearized
model near an equilibrium point, we compute the linearization at 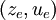
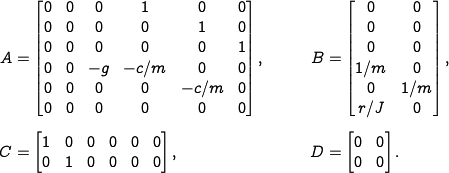
Letting 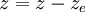 and
and 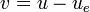 , the linearized system is
given by
, the linearized system is
given by
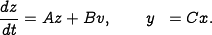
It can be verified that the system is reachable.
To compute a linear quadratic regulator for the system, we write the cost function as
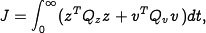
where 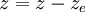 and
and 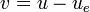 represent the local coordinates
around the desired equilibrium point
represent the local coordinates
around the desired equilibrium point 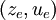 . We begin with
diagonal matrices for the state and input costs:
. We begin with
diagonal matrices for the state and input costs:

This gives a control law of the form 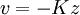 , which can then be
used to derive the control law in terms of the original variables:
, which can then be
used to derive the control law in terms of the original variables:
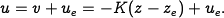
The equilibrium points
have 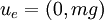 and
and 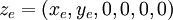 . The
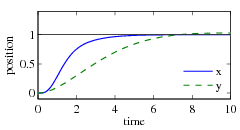
response of the closed loop system to a step change in the desired position is
shown below.
. The
response of the closed loop system to a step change in the desired position is
shown below.
|
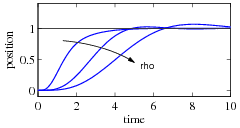
| |
Step response in 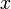 and and 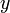
|
Effect of control weight 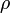
|
The plot on the left shows the 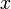 and
and 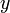 positions of the aircraft when it is
commanded to move 1 m in each direction.
The response can be tuned by adjusting the weights in the LQR cost.
The plot on the right shows
the
positions of the aircraft when it is
commanded to move 1 m in each direction.
The response can be tuned by adjusting the weights in the LQR cost.
The plot on the right shows
the 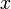 motion for control weights
motion for control weights  ,
, 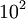 ,
,  . A higher weight of the input term
in the cost function causes a more sluggish response.
. A higher weight of the input term
in the cost function causes a more sluggish response.
Lateral control using inner/outer loop design
To control the lateral dynamics of the vectored thrust aircraft, we make use of a "inner/outer" loop design methodology. This example is drawn from Chapter 11 - Frequency Domain Design.
- pvtol_nested.m - MATLAB code used to produce figures in this example
- pvtol_params.m - parameter definitions
We begin by representing the dynamics using the block diagram

where
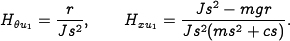
The controller is constructed by splitting the process dynamics and controller into
two components: an inner loop
consisting of the roll dynamics 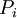 and
control
and
control 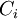 and an outer loop consisting
of the lateral position
dynamics
and an outer loop consisting
of the lateral position
dynamics 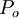 and controller
and controller  .
.
The closed inner loop dynamics  control the roll angle of the aircraft using
the vectored thrust while the outer loop controller
control the roll angle of the aircraft using
the vectored thrust while the outer loop controller  commands the
roll angle to regulate the lateral position. As a performance specification for the entire system,
we would like to have zero steady-state error in the lateral position,
a bandwidth of approximately 1 rad/s and a phase
margin of 45°.
commands the
roll angle to regulate the lateral position. As a performance specification for the entire system,
we would like to have zero steady-state error in the lateral position,
a bandwidth of approximately 1 rad/s and a phase
margin of 45°.
Inner loop design
For the inner loop, we choose our design specification to provide the outer loop with accurate and fast control of the roll. The inner loop dynamics are given by
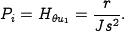
We choose the desired bandwidth to be 10 rad/s (10 times that of the outer loop) and the low-frequency error to be no more than 5%. To achieve our performance specification, we would like to have a gain of at least 10 at a frequency of 10 rad/s, requiring the gain crossover frequency to be at a higher frequency. We see from the loop shape below (left) that in order to achieve the desired performance we cannot simply increase the gain since this would give a very low phase margin. Instead, we must increase the phase at the desired crossover frequency.
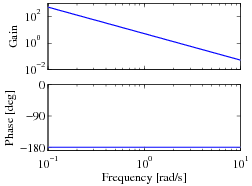
|
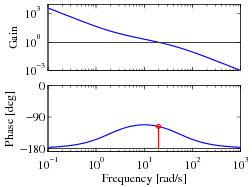
|
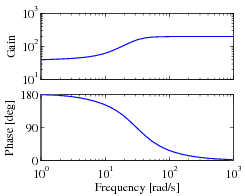
|
| Open loop roll dynamics | Loop transfer function with lead compensator | Closed loop roll dynamics |
To accomplish this, we use a lead
compensator with 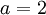 and
and 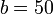 :
:
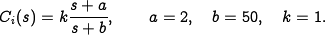
We then set the gain of the system to provide a large loop gain up to the desired bandwidth, as shown above (center). We see that this system has a gain of greater than 10 at all frequencies up to 10 rad/s and that it has more than 60° of phase margin.
The resulting closed loop dynamics for the system satisfy
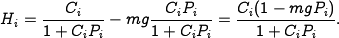
A plot of the magnitude of this transfer function is shown above (right), and we see that 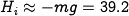 is a good approximation up to 10 rad/s.
is a good approximation up to 10 rad/s.
Outer loop design
To design the outer loop controller, we assume the inner loop roll
control is perfect, so that we can take 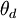 as the input to our
lateral dynamics. The outer loop dynamics can be
written as
as the input to our
lateral dynamics. The outer loop dynamics can be
written as
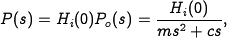
where we replace 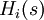 with
with  to reflect our approximation
that the inner loop will eventually track our commanded input. Of
course, this approximation may not be valid, and so we must verify this
when we complete our design.
to reflect our approximation
that the inner loop will eventually track our commanded input. Of
course, this approximation may not be valid, and so we must verify this
when we complete our design.
Our control goal is now to design a controller that gives zero
steady-state error in  and has a bandwidth of
1 rad/s. The outer loop process dynamics are
given by a second-order integrator, and we can again use a simple lead
compensator to satisfy the specifications. We also choose the design
such that the loop transfer function for the outer loop has
and has a bandwidth of
1 rad/s. The outer loop process dynamics are
given by a second-order integrator, and we can again use a simple lead
compensator to satisfy the specifications. We also choose the design
such that the loop transfer function for the outer loop has 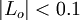 for
for 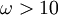 rad/s, so that the
rad/s, so that the  dynamics can be neglected. We choose the controller to be of the form
dynamics can be neglected. We choose the controller to be of the form
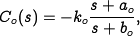
with the negative sign to cancel the negative sign in the process
dynamics. To find the location of the poles, we note that the phase
lead flattens out at approximately 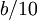 . We desire phase lead at
crossover, and we desire the crossover at
. We desire phase lead at
crossover, and we desire the crossover at 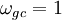 rad/s, so
this gives
rad/s, so
this gives 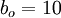 . To ensure that we have adequate phase lead, we
must choose
. To ensure that we have adequate phase lead, we
must choose 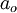 such that
such that 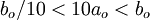 , which implies that
, which implies that 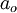 should be between 0.1 and 1. We choose
should be between 0.1 and 1. We choose 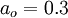 . Finally, we need
to set the gain of the system such that at crossover the loop gain has
magnitude 1. A simple calculation shows that
. Finally, we need
to set the gain of the system such that at crossover the loop gain has
magnitude 1. A simple calculation shows that 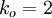 satisfies
this objective. Thus, the final outer loop controller becomes
satisfies
this objective. Thus, the final outer loop controller becomes
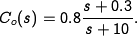
Complete system analysis
Finally, we can combine the inner and outer loop controllers and verify that the system has the desired closed loop performance. The Bode and Nyquist plots with inner and outer loop controllers are shown below Figure~\ref{fig:pvtol:nested-plots}, and we see that the specifications are satisfied.
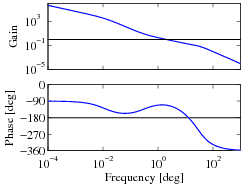
|
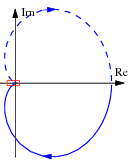
|
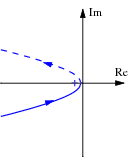
|
| Bode plot for combined controller | Nyquist plot for combined controller | Zoomed in Nyquist plot |
The system has a phase margin of 68° a gain margin of 6.2.
To better understand the properties of the closed loop system, we can generate the Gang of Four:
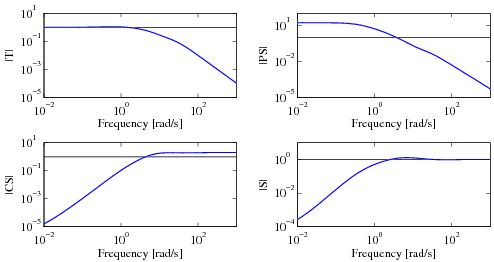
We see that the transfer functions
between all inputs and outputs are reasonable.
The sensitivity to load disturbances 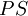 is large at low frequency because
the controller does not have integral action.
is large at low frequency because
the controller does not have integral action.
The approach of splitting the dynamics into an inner and an outer loop is
common in many control applications and can lead to simpler designs
for complex systems. Indeed, for the aircraft dynamics studied in
this example, it is very challenging to directly design a controller from the
lateral position 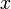 to the input
to the input 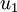 . The use of the additional
measurement of
. The use of the additional
measurement of 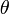 greatly simplifies the design because it can
be broken up into simpler pieces.
greatly simplifies the design because it can
be broken up into simpler pieces.