Phase locked loop

A phased locked loop is a system which generates a sinusoidal signal

that is synchronised with a given periodic system. Phase-locked loops are widely used in electronic systems, they are key components in wireless communication systems and in optical drives. The systems are used to generate a sinusoidal signal or other periodic signal that is synchronized with a given periodic signal.

Modeling

A schematic diagram of a phase-locked loop is shown below:

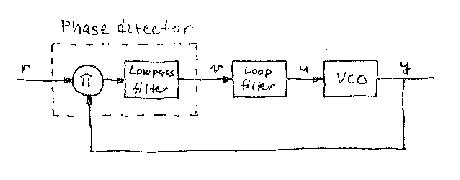
The system consists of a phase detector, a voltage controlled oscillator and a filter. A multiplier combined with a low pass filter is a simple phase detector. To analyze the system we assume that the the input voltage 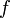and the output 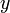of the voltage controlled oscillator are sinusoidal signals

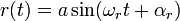
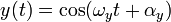
The product of the input and the output signals are

	=

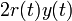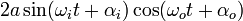
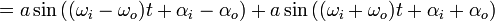
In the ideal case the frequencies 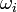and 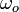are both equal to 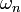, in practice the frequencies are close. The first term then has low frequency and the second term has high frequency. The low pass filter and the voltage controlled oscillator will attenuate the high frequency component and we get approximately

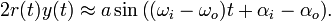
Introducing the phases 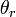and 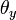of the input and output signals defined by

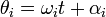
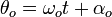
we find that the phase detector consisting of a multiplier and a low pass filter can be modeled by

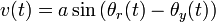
Assuming that the frequency of the voltage controlled oscillator is proportional to its input we find that it can be modeled by

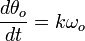
The complete system can then be represented by the block diagram shown below

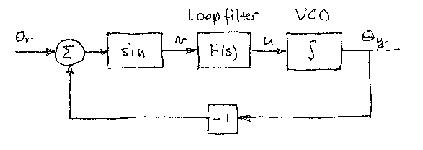
Notice that the gain of the loop is proportional to the amplitude of the input signal. The loop filter is designed to make the sure that the derivative of the output tracks the derivative of the input 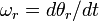. It is required that the system can find the frequency of an input signal (signal acquisition) and that it can track a signal with slowly varying frequency (regulation).

Simulation

The figure below shows a simulation of a phase-locked loop where the filter is a PI controller.

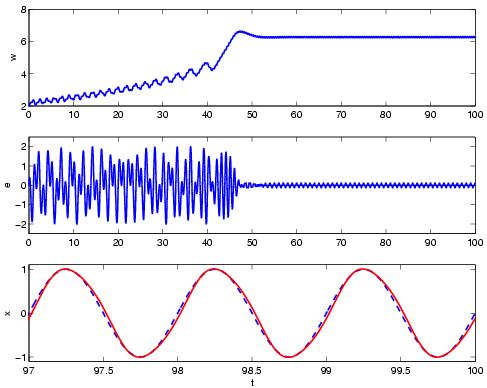
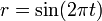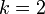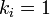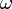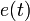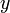The input signal is and the controller parameters are and . The top curve shows the frequency , the middle curve shows the error and the bottom curves show the input signal (dashed) and the output signal (full). Notice that the frequency converges to the correct value. There is a small high frequency oscillation of the frequency and a small distortion of the output wave form. These defects can be eliminated by an improved filter.

The phase-locked loop is a nice example of how block diagram structuring and approximations can help us understand and design a complex system. Also notice the appearance of a sine function, which makes design of a phase-locked loop similar to design of a stabilizer for an inverted pendulum.