Delta-sigma converter

Delta-sigma converters are used for analog to digital conversion in high-quality audio and communications equipment. Common examples are one-bit A/D converters and digital audio amplifiers. Delta-sigma converters are also used to generate pulse-width modulated signals for motor drives. The converter generates an output signal with quantized amplitude that resembles the input signal in the sense that the filtered output is close to the input. In the extreme case of a one-bit converter the output has only two levels.

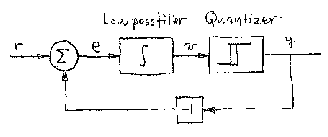
A schematic diagram of a delta-sigma converter is shown below.

The system is a feedback loop with a quantizer and a low pass filter. A particularly simple version is when the quantizer is a relay with hysteresis and the filter is an integrator.

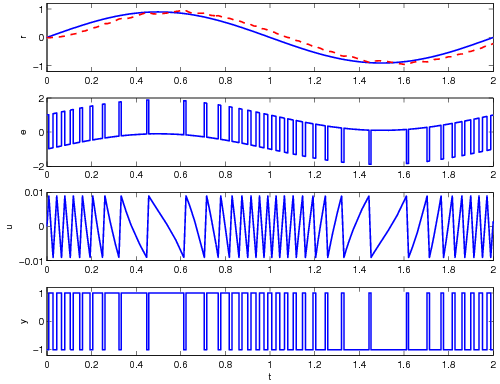
The figure below shows a simulation of such a converter when the input is a sinusoid.

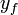The upper curve shows the input (full) and the filtered output (dashed); the next curves show the error , the filtered error 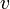and the converter output 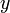. The loop filter is an integrator, the quantizer a relay with hysteresis 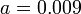. The pulse output 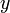is filtered with a second order low-pass filter with time constant 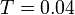s.

A feedback loop will normally act to make the error small. In this particular case the instantaneous value cannot be made small because the output switches between -1 and 1. The integral of the error is however small because it can be shown that

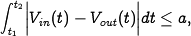
where the interval 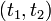covers a full cycle, and 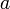is the hysteresis of the relay. The filtered output 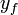is also close to the input .

Digital signals are formed by sampling in time and by quantization in amplitude. The delta-sigma modulator shows that a good digital representation can be obtained with a crude quantization of the amplitude, only 0 and 1, provided that the time resolution is sufficiently high (oversampling). The pulsed output signal is an interesting signal form. It encodes the original continuous signal into a pulse-width modulated signal where the average value corresponds to the signal amplitude. The pulse width is proportional to the rate of change of the continuous signals. Pulsed signals of this sort are common in biological systems.

Exercise: Propose a way to obtain an estimate of the instantaneous value of the reference signal and its derivative from the pulsed output.