The amazingly rich structure of the solutions of the first Painlevé equation, the very simple differential equation .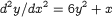

Hans Duistermaat

Abstract: The differential equation 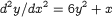is the first in Painlevé's classification of those algebraic second order ordinary differential equations such that every isolated singularity of moderate growth of every solution is a pole. Despite the simple form of the first Painlevé equation, the analysis of its solutions is very subtle. Painlevé thought in 1900 to have proved that every solution can be extended to a meromorphic function on the whole complex x--plane, but the first complete proofs were only given almost a century later. Boutroux discovered in 1913 a transformation to an approximately autonomous differential equation, which allowed him to draw spectacular conclusions about the asymptotic behavior of the locations of the poles near infinity in the complex plane. His proofs contained serious gaps and errors, but his conclusions were basically correct, and can be strengthened considerably. In this talk I would like to report on my joint work in progress with Nalini Joshi on this.

The first Painlevé equation can also be obtained as a compatibility condition between two linear systems of ordinary differential equations, one in the variable x with a parameter 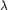, and the other with the roles of x and 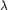interchanged. This has been used to study the asymptotic properties of the first Painlevé transcendants, but our analysis does not use this, in the literature called "isomonodromy method".