Claudia Wulff: Abstract

We prove that a class of A-stable symplectic Runge--Kutta time semidiscretizations (including the Gauss--Legendre methods) applied to a class of semilinear Hamiltonian PDEs which are well-posed on spaces of analytic functions conserve a modified energy of analytic initial data up to an exponentially small error. This modified energy is 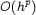-close to the original energy where 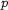is the order of the method and 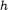the time step-size. Examples of such systems are the semilinear wave equation or the nonlinear Schrödinger equation with analytic nonlinearity and periodic boundary conditions. Standard backward error analysis can not be applied because of the occurrence of unbounded operators in the construction of the modified vector field. This loss of regularity in the construction can be taken care of by projecting the PDE to a finite-dimensional space and by coupling the number of excited modes as well as the number of terms in the expansion of the vectorfield with the stepsize. This way we obtain exponential estimates of the form $O(\e^{ -\beta/h^{1/(1+q)}})$, 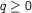, 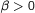. In the case of the wave equation 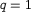and for the nonlinear Schrödinger equation, 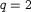. As a side-product, we also provide a convergence analysis of implicit Runge--Kutta methods in Hilbert spaces.

back