The Anisotropic Lagrangian Averaged Euler and Navier-Stokes Equations

Marsden, J. E. and S. Shkoller

Arch. Rational Mech. Anal. 166, 27-46.

Abstract:

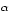
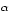
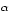
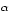
The purpose of this paper is twofold. First, we give a derivation of the Lagrangian averaged Euler (LAE-$\alpha$) and Navier-Stokes (LANS-$\alpha$) equations. This theory involves a spatial scale $\alpha$ and the equations are designed to accurately capture the dynamics of the Euler and Navier-Stokes equations at length scales larger than $\alpha$, while averaging the motion at scales smaller than $\alpha$. 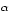The derivation involves an averaging procedure that combines ideas from both the material (Lagrangian) and spatial (Eulerian) viewpoints. This framework allows the use of a variant of G. I. Taylor's "frozen turbulence" hypothesis as the foundation for the model equations; more precisely, the derivation is based on the strong physical assumption that fluctutations are frozen into the mean flow. 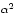In this article, we use this hypothesis to derive the averaged Lagrangian for the theory, and all the terms up to and including order $\alpha^{2}_{}$ are accounted for.

The equations come in both an isotropic and anisotropic version. The anisotropic equations are a coupled system of PDEs (partial differential equations) for the mean velocity field and the Lagrangian covariance tensor. In earlier works by FOIAS, HOLM & TITI [10], and ourselves [16], an analysis of the isotropic equations has been given. In the second part of this paper, we establish local in time well-posedness of the anisotropic LANS-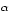$\alpha$ equations using quasilinear PDE type methods.