The absence of Killing fields is necessary for linearization stability of Einstein's equations

Arms, J. M. and J. E. Marsden

Indiana University Math. J., 28, (1979), 119-125

Abstract:

The purpose of this paper is to discuss the proofs of Theorem 1 and 2 below.

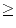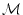
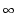
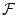
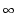
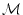
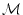
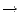
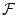
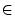
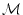
Theorem 1. Let M be a compact, connected, oriented smooth manifold with dim M $\geq$ 3 . Let $\mathcal {M}$ be the space of C^$\infty$ [or W^{s, p}, s > (n/p) + 1 ] riemannian metrics on M , let $\mathcal {F}$ denote the C^$\infty$ [or W^{s-2, p} ] scalar functions on $\mathcal {M}$ and let R : $\mathcal {M}$$\to$$\mathcal {F}$ be the scalar curvature map. Also suppose that g₀ $\in$ $\mathcal {M}$ and 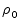$\rho_{{0}}^{{}}$ = R(g₀) . Then the equation R(g) = 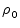$\rho_{0}^{}$ is linearization stable at g₀ if and only if DR(g₀) is surjective.

In the definition of linearization stability we use the C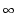^$\infty$ (or H^s ) topology on compact subsets of V₄ .

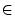
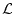
Theorem 2. Let Ein(⁽⁴⁾g₀) = 0 for ⁽⁴⁾g₀ $\in$ $\mathcal {L}$ . Then ⁽⁴⁾g₀ is linearization stable if and only if ⁽⁴⁾g₀ has no Killing fields.