General relativity as a dynamical system on the manifold a of Riemannian metrics which cover diffeomorphisms

Fischer, A. E. and J. E. Marsden

Springer Lecture Notes in Physics, 14, (1972), 176-188

Abstract:

In this paper we consider the geometrodynamical formulation of general relativity, due most recently to Arnowitt, Deser, and Misner [2], Dewitt [3], and Wheeler [8], from the point of view of manifolds of maps (function spaces) and infinite-dimensional geometry.
Hydrodynamics is approached from this point of view by Arnold [1] and be Ebin-Marsden [4]; in Fischer-Marsden [5, 6] the function spaces appropriate for a dynamical formulation of general relativity are introduced. We hope that our approach will clarify the basic dynamical structure of the Einstein equations and the associated infinite-dimensional geometry in a spirit analogous to that which has been done in hydrodynamics.
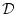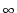
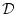
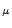
The key to our approach is the group $\mathcal {D}$ = Diff(M) of smooth ( C^$\infty$ ) diffeomorphisms of a fixed 3-dimensional manifold M . For hydrodynamics one concentrates on $\mathcal {D}$_$\mu$ , the volume preserving diffeomorphisms Ebin-Marsden [4]. For relativity one uses the manifold a of Riemannian metrics which cover diffeomorphisms.
We begin with a description of a.