Exercise: Modeling and simulation of an exothermic reaction
(Contributed by Anand Asthagiri, 3 Oct 04)
Consider a chemical reactor in which species A undergoes a first-order, exothermic conversion to species B. To remove the heat of reaction, a jacket surrounds the reactor where a coolant is maintained at 100 deg F. Suppose that such a reactor is performing at steady-state conditions provided in the table below:
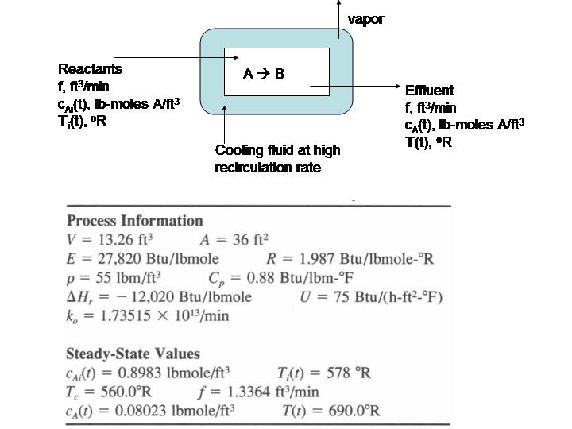
Inevitably, under normal process conditions, the reactor will experience
disturbances in the inlet temperature (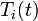
) and concentration of species
A (
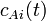) in the input stream. Thus, we would like to know what impact
these fluctuations in inlet conditions might have on the concentration of
species A (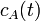
) and the temperature (
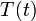) of the effluent stream.
Suggestions: Assume that the reactor contents are well-mixed and that the heat
capacity (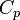
) and density (
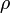) of reactants and products are equal.
Develop a set of equations that could be used to predict temporal changes in effluent temperature and species A concentration (
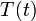and
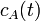, respectively).
Since we are interested in deviations in process variables, it is useful to reformulate the above equations in terms of deviation variables. A deviation variable (
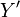) for a process variable (
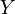) is defined as 
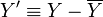where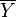 
is the steady-state value. Reformulate
equations in terms of such deviation variables, and solve for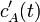 
and
.
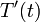</li>Plot
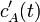and 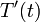versus time for the following cases: (a)
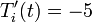deg R and (b) 
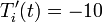deg R. Explain the
observed behavior of the reactor. Does it always return to the same
steady-state value? Is the dynamic response ``smooth or oscillatory?
</li>
