


Next: About this document ...
documentclass[11pt]article
usepackageamssymb,amsmath,latexsym
usepackagegraphicx
par
newedcommandbfibfseriesitshape
par
textwidth 6.5 truein
oddsidemargin 0 truein
evensidemargin -0.50 truein
topmargin -.5 truein
textheight 8.5in
par
newedtheoremthmTheorem[section]
newedtheoremprop[thm]Proposition
newedtheoremlem[thm]Lemma
newedtheoremcor[thm]Corollary
newedtheoremdfn[thm]Definition
par
newedcommandintprod[2]#1hook#2
newedcommandhookmathbinhboxvrule height .5pt width 3.5pt depth 0pt
vrule height 6pt width .5pt depth 0pt
par
makeatletter
addtoresetfiguresubsection
addtoresettablesubsection
addtoresetequationsubsection
makeatother
par
makeatletter
par
newskip centering
centering = 0pt plus 1000pt
par
eqnsel=
par
makeatother
par
begindocument
par
titleReview: Vector Spaces
par
authorCDS201 Lecturer: W.S. Koon
datesmall Fall, 1998
maketitle
par
sectionReal and Complex Vector Spaces
paragraphDefinition:
paragraphExamples:
beginenumerate
item 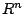 item
item 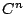 item
item ![$ C[0,1]$](img3.gif) item
item ![$ L^2[0,1]$](img4.gif) item matrices
item polynomials
endenumerate
par
sectionSubspace
paragraphDefinition:
paragraphExamples:
beginenumerate
item Let
item matrices
item polynomials
endenumerate
par
sectionSubspace
paragraphDefinition:
paragraphExamples:
beginenumerate
item Let  be any vector space,
be any vector space,  is a subspace of
is a subspace of  and
and
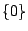 is a subspace of
is a subspace of  .
item
.
item 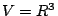 ,
,
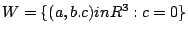 .
item
.
item 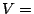 space of
space of 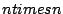 matrices,
matrices, 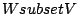 is the subset of
symmetric matrices.
item
is the subset of
symmetric matrices.
item  is the set of all polynomials of degree
is the set of all polynomials of degree 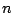 with real coefficients,
with real coefficients,
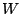 is the subset of
is the subset of  consisting of polynomials of degree
consisting of polynomials of degree
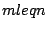 .
item
.
item 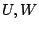 subspaces of
subspaces of  ,
, 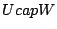 is a subspace of
is a subspace of  .
endenumerate
par
sectionLinear Combinations and Spans
paragraphDefinition: Let
.
endenumerate
par
sectionLinear Combinations and Spans
paragraphDefinition: Let  be a vector space,
be a vector space,
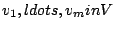 .
Any vector in
.
Any vector in  of the form
of the form
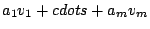 is called a it
linear combination of
is called a it
linear combination of
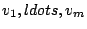 .
.
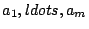 are called the
coefficients of the linear combinations.
par
paragraphDefinition: Let
are called the
coefficients of the linear combinations.
par
paragraphDefinition: Let 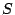 be a subset of a vector space
be a subset of a vector space  .
. 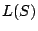 denotes the set of all linear combinations of vectors in
denotes the set of all linear combinations of vectors in 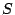 . It can be
shown that
. It can be
shown that 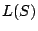 is a subspace, and it is said to be the subspace it
spanned or generated by
is a subspace, and it is said to be the subspace it
spanned or generated by 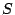 .
par
sectionDirect Sum
paragraphDefinition: Suppose
.
par
sectionDirect Sum
paragraphDefinition: Suppose 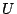 and
and 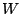 are subspace of a vector space
are subspace of a vector space
 . Then the sum of
. Then the sum of 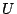 and
and 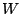 , denoted
, denoted 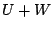 , consists of all sums
, consists of all sums
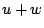 where
where 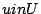 ,
, 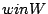 , i.e.
par
paragraphDefinition:
, i.e.
par
paragraphDefinition:  is said to be the it direct sum
of
is said to be the it direct sum
of 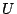 and
and 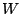 if
for any
if
for any 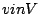 there exists a unique
there exists a unique
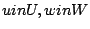 such that
such that 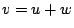 .
.
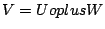 .
par
paragraphExamples:
.
par
paragraphExamples: 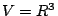 beginenumerate
item
beginenumerate
item
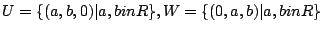 . Notice that while
. Notice that while
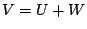 ,
,  is not the direct sum of
is not the direct sum of 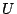 and
and 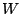 .
item
.
item
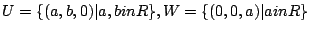 .
.
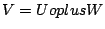 .
endenumerate
par
begintheorem_type[prop][thm][][][][]
Suppose
.
endenumerate
par
begintheorem_type[prop][thm][][][][]
Suppose 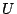 and
and 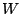 are subspaces of
are subspaces of  . Then
. Then 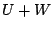 is also a subspace of
is also a subspace of
 .endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
Let
.endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
Let 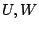 be subspaces of a vector space
be subspaces of a vector space  . Then
. Then  is a direct sum of
is a direct sum of 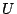 and
and 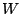 if and only if
beginenumerate
item
if and only if
beginenumerate
item 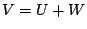 item
item
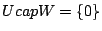 .
endenumerateendtheorem_type
vspace2in
par
sectionLinear Independence and Dependence
paragraphDefinition: Let
.
endenumerateendtheorem_type
vspace2in
par
sectionLinear Independence and Dependence
paragraphDefinition: Let  be a vector space and let
be a vector space and let
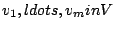 . The set
. The set
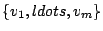 is said to be
it linearly independent
if
is said to be
it linearly independent
if
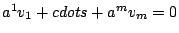 implies
implies
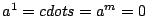 . Otherwise,
they are said to be it linearly dependent.
par
paragraphExample: Linear dependence in
. Otherwise,
they are said to be it linearly dependent.
par
paragraphExample: Linear dependence in 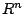 Problem of linear dependence
is related to a nontrivial solution of a homogeneous system of linear
equations.
par
begintheorem_type[prop][thm][][][][]
Let
Problem of linear dependence
is related to a nontrivial solution of a homogeneous system of linear
equations.
par
begintheorem_type[prop][thm][][][][]
Let
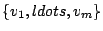 be a collection of nonzero vectors. Then this set
of vectors is linearly dependent if and only if one of the vectors can be
expressed as a linear combination of the others.endtheorem_type
vspace1in
par
sectionBases, Coordinates and Dimension
paragraphDefinition: Let
be a collection of nonzero vectors. Then this set
of vectors is linearly dependent if and only if one of the vectors can be
expressed as a linear combination of the others.endtheorem_type
vspace1in
par
sectionBases, Coordinates and Dimension
paragraphDefinition: Let
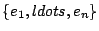 be a set of linearly
independent vectors in a vector space
be a set of linearly
independent vectors in a vector space  . Then
. Then
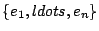 is said to be a it basis for
is said to be a it basis for  if any
if any 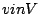 can be expressed as a
linear combination of
can be expressed as a
linear combination of
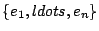 , i.e.
, i.e.
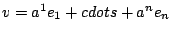 .
The numbers
.
The numbers
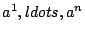 are called the components or it coordinates
of the vector
are called the components or it coordinates
of the vector 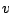 with respect to the basis
with respect to the basis
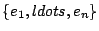 .
The components are unique for a given basis.
par
paragraphDefinition: A vector space
.
The components are unique for a given basis.
par
paragraphDefinition: A vector space  is said to have dimension
is said to have dimension 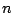 if
it has
if
it has 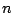 linearly independent vectors while every set of
linearly independent vectors while every set of 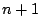 vectors
are linearly dependent.
par
begintheorem_type[thm][thm][section][][][]
In a vector space
vectors
are linearly dependent.
par
begintheorem_type[thm][thm][section][][][]
In a vector space  of dimension
of dimension 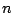 there exists a basis consisting of
there exists a basis consisting of 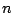 independent vectors. Moreover, any set of
independent vectors. Moreover, any set of 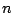 linearly independent vectors
in
linearly independent vectors
in  is a basis for
is a basis for  .endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
If there is a basis in
.endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
If there is a basis in  , then the dimension of
, then the dimension of  equals the number of
basis vectors.endtheorem_type
vspace5in
par
sectionUseful Theorems Concerning Subspaces and Bases
begintheorem_type[thm][thm][section][][][]
Suppose
equals the number of
basis vectors.endtheorem_type
vspace5in
par
sectionUseful Theorems Concerning Subspaces and Bases
begintheorem_type[thm][thm][section][][][]
Suppose 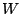 is a subspace of the vector space
is a subspace of the vector space  where dim
where dim 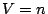 and let
and let
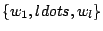 be a basis for
be a basis for 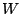 . Then there exists vectors
. Then there exists vectors
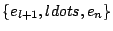 such that
such that
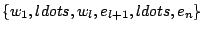 is a basis of
is a basis of  .endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
Suppose
.endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
Suppose 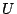 and
and 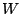 are subspaces of a finite dimensional vector space
are subspaces of a finite dimensional vector space  .
Then dim
.
Then dim 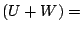 dim
dim 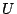 + dim
+ dim 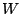
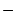 dim
dim 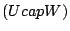 .endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
Let
.endtheorem_type
par
begintheorem_type[thm][thm][section][][][]
Let  be a vector space of dimension
be a vector space of dimension 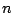 and suppose
and suppose 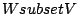 is a
subspace of
is a
subspace of  . Then there exists a subspace
. Then there exists a subspace 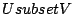 such that
such that
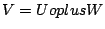 .endtheorem_type
enddocument
.endtheorem_type
enddocument



Next: About this document ...
www admin
1998-09-28