Discrete Euler-Poincaré and Lie-Poisson Equations

Marsden, J. E., S. Pekarsky, and S. Shkoller

Nonlinearity, 12, 1647-1662.

Abstract:

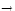
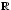
In this paper, discrete analogues of Euler-Poincaré and Lie-Poisson reduction theory are developed for systems on finite dimensional Lie groups G with Lagrangians L : TG $\rightarrow$ $\mathbb {R}$ that are G-invariant. These discrete equations provide ``reduced'' numerical algorithms which manifestly preserve the symplectic structure. 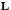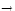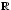The manifold G x G is used as an approximation of TG, and a discrete Langragian $\mathbb {L}$ : G x G $\rightarrow$ $\mathbb {R}$ is constructed in such a way that the G-invariance property is preserved. 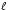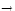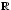Reduction by G results in new ``variational'' principle for the reduced Lagrangian $\ell$ : G $\rightarrow$ $\mathbb {R}$, and provides the discrete Euler-Poincaré (DEP) equations. Reconstruction of these equations recovers the discrete Euler-Lagrange equations developed in [#!MPS!#,#!WM!#] which are naturally symplectic-momentum algorithms. Furthermore, the solution of the DEP algorithm immediately leads to a discrete Lie-Poisson (DLP) algorithm. 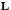It is shown that when G = SO(n), the DEP and DLP algorithms for a particular choice of the discrete Lagrangian $\mathbb {L}$ are equivalent to the Moser-Veselov scheme for the generalized rigid body.