Both upper and lower estimates are established for the separatrix splitting of rapidly forced systems with a homoclinic orbit. The general theory is applied to the equation
for illustration. There are two types of results. First, fix
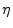 > 0
> 0
and let
0 < 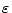
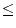 1
1
and
0 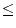
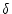
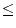
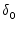
where
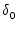
is sufficiently small. If the separatrices split, they do so by an amount that is no more than
where
C = C(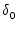 )
)
is a constant depending on
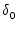
but is uniform in
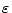
and
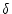
. Second, if we replace
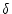
by
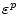
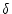
, with
p 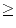 8
8
, then we have the sharper estimate
for positive constants
C1
and
C2
depending on
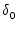
alone. In particular, in this second case, the Melnikov criterion correctly predicts exponentially small splitting and transversal intersection of the separatrices. After developing this theory we discuss some of its applications, concentrating on a
2 : 1
resonance that occurs in a KAM (Kolmogorov, Arnold, and Moser) situation and in the forced saddle node bifurcation described by
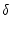 exp
exp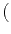 -
- 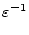 (
(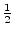
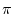 -
- 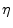 )
)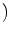
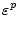
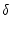 e-
e-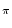
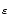 /2
/2 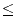 splitting distance
splitting distance 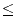 C1
C1 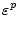
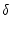 e-
e-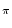
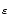 /2
/2