Generic Bifurcation of Hamiltonian Systems with Symmetry

Marsden, J. E.

appendix to Golubitsky and Stewart, Physica D, 24, (1987), 391-405

Abstract:

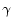
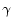
We study generic bifurcation of equilibria in one-parameter Hamiltonian systems with symmetry group $\gamma$ where eigenvalues of the linearized system go through zero. Theorem 3.3 classifies expected actions of $\gamma$ on the generalized eigenspace of this zero eigenvalue. Generic one degree of freedom symmetric systems are classified in section 4; remarks concerning systems with more degrees of freedom are given in section 5.